티스토리 뷰
오늘은 전기 소자 중 하나인 '인덕터(Inductor)'에 대해서 알아보겠습니다.
앞 서, 저항과 커패시터에 대해서 기본 개념과 역할에 대해서 포스팅을 했는데요,
이제 전기소자에서 마지막으로 소개하는 '인덕터(Inductor)'까지 보면 R, L, C 전부 알게 되는 것이죠!

※저항이란? 쉽게 이해하기
[전기회로] 저항이란? 옴의 법칙, 저항 계산법
0. 포스팅을 시작하며 안녕하세요 우물 안 커밋입니다 :) 오늘은 전자회로를 입문하기 전에 배우는 '전기 소자'중에 하나인 '저항(Resistance), 저항기(Resistor)'에 대해서 알아보겠습니다. 이 글을 시
ekzkdtl.tistory.com
※커패시터란? 쉽게 이해하기
[전기회로] 커패시터란? 커패시턴스란? 커패시터 공식, 커패시터 계산법
0. 포스팅을 시작하며 안녕하세요 우물 안 커밋입니다 :) 오늘은 전기 소자 중 하나인 '커패시터(Capacitor)' / '콘덴서(condenser)에 대해서 알아보겠습니다. 저항만큼이나 전자 제품에서 빠짐없이 사
ekzkdtl.tistory.com
※인덕터의 역할 한방에 이해하기
[전기회로] 인덕터의 역할 (LC 필터, 전원 안정화)
오늘은 인덕터의 역할에 대해서 알아보겠습니다. 전에 포스팅한 내용과 연결되는 부분이니, 아래 링크 확인하시면 더욱 도움 되실 겁니다 :) [전자회로] 인덕터란? 인덕턴스란? 인덕터 공식, 인
ekzkdtl.tistory.com
1. '인덕턴스(Inductance), 인덕터(Inductor)'란?

인덕턴스(Inductance)란, 코일에 흐르는 전류의 시간에 따른 변화와 그로 인하여 유도되는 역기전력, 유도기전력의 비율을 인덕턴스라고 정의한다. 단위는 H(헨리)이다.
※역기전력, 유도기전력이란? : 코일에 흐르는 전류가 변화하면 그 변화를 방해하는 방향으로 전압을 유도하는 현상
-출처 naver 지식 백과
위의 설명처럼,
'인덕턴스(Inductance)'는 전류가 변화할 때 그 변화를 방해하는 역기전력의 비율을 나타내는 물리량입니다.
이러한 특성을 활용하여, 필요한 인덕턴스값을 얻기 위한 부품이 '인덕터(Inductor)'입니다.
즉, '인덕터(Inductor)'는 전류의 변화량에 비례해 전압을 유도하는 전기 부품입니다.
2. 인덕턴스, 유도 기전력, 인덕터 공식
1) 인덕턴스 공식?

인덕턴스 공식은, '코일에 생성되는 자속(Φ) 은 코일에 흐르는 전류(I)와 비례한다'는 식으로 부터 시작됩니다.
'Φ ∝ I'
코일의 감은 권수가 N이면 코일에 생성되는 전체 자속은 NΦ가 됩니다.
'NΦ ∝ I'
보통은 비례식을 표현할 때 비례 상수를 곱해주는데 이때! 비례 상수가 바로 인덕턱스(L)입니다.
'NΦ = LI'
즉, 인덕턴스 공식은 L=NΦ/I가 됩니다.

식을 통해서 알 수 있듯이, 전류(I)가 흐를 때 발생하는 자속(NΦ)은 인덕턴스(L)값에 의해 결정이 됩니다.
즉, 인덕턴스(L)값이 크면 클수록, 전류를 자속(NΦ)으로 변환하는 양도 커지겠죠?? (똑같은 전류가 흐를 경우)
2) 유도 기전력 공식?
인덕턴스(L)는 유도기전력을 빼놓고 얘기할 수 없습니다.
앞 서, 유도기전력(E)은 자속(Φ)을 방해하는 반대 방향으로 발생한다고 설명드렸습니다.
따라서, 유도기전력 식은 다음과 같이 표현할 수 있습니다.

위 공식에 인덕턴스 공식인 'NΦ =LI'을 대입해보면,

3) 인덕터 전류-전압 공식?
유도기전력 E 공식을 통해서,
인덕터(L)의 전압(V)을 식으로 표현하면 다음과 같습니다.

양단을 적분하여 전류(I) 식으로 표현하면 다음과 같습니다.

! 공식 정리!
1) 인덕턴스 공식

2) 유도 기전력 공식

3) 인덕터 전류-전압 공식


3. 인덕터 계산법
인덕터는 크게 1) 직렬연결 2) 병렬 연결로 나눌 수 있습니다.
각각의 연결 방식에 따라 인덕터 계산하는 식이 다릅니다.
그림을 통해서 쉽게 보겠습니다.
1) 인덕터의 직렬 연결
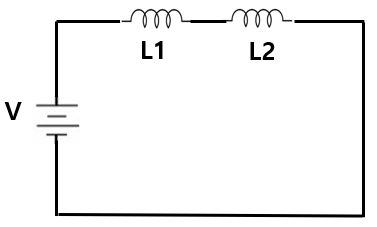
위의 그림처럼 인덕터가 직렬로 연결되어 있는 상태에서
전체 인덕터(L)는 각 인덕터의 합(L1 + L2)과 같습니다.
식으로 표현하면 다음과 같습니다.
전체 L = L1 + L2 + L3 + ...+Ln
2) 인덕터의 병렬연결
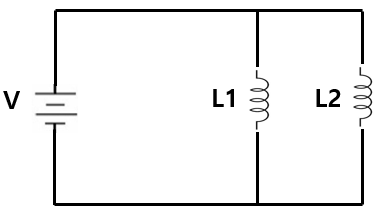
위의 그림처럼 인덕터가 병렬로 연결되어 있는 상태에서
전체 인덕터의 역수(1/L)는 각 인덕터 역수의 합(1/L1 + 1/L2)과 같습니다.
식으로 표현하면 다음과 같습니다.
1/전체 L = 1/L1 + 1/L2 + 1/L3 + ...+1/Ln
앞 서 저항의 연결 방식에 따른 계산 식을 봤었는데요, 인덕터는 저항과 똑같다고 기억하시면 됩니다!
이번 포스팅에서는 '인덕턴스', '인덕터'의 기초적인 내용에 대해서 알아봤습니다.
다음 포스팅에서는 실무에서 실제 어떤 용도와 역할로 사용되는지 자세히 소개하겠습니다.
오늘도 좋은 하루 보내시고 항상 건강하세요!! :)

'IT 정보 > 전기회로' 카테고리의 다른 글
| [전기회로] 저항의 종류와 특징 - 실제 실무에서 사용되는 것 (24) | 2023.05.14 |
|---|---|
| [전기회로] 인덕터의 역할 (LC 필터, 전원 안정화) (36) | 2023.05.02 |
| [전기회로] 커패시터의 역할 (바이패스, 벌크, 커플링, 디커플링 커패시터) (57) | 2023.04.29 |
| [전기회로] 커패시터란? 커패시턴스란? 커패시터 공식, 커패시터 계산법 (28) | 2023.04.28 |
| [전기회로] 저항의 역할 (전류 제한, 전압 분배, Pull up, Pull down) (26) | 2023.04.24 |